1、HashMap数据结构
2、数据的增删改查
(1)存数据put(K key, V value)
(2)取数据get(Object key)
(3)删数据remove(Object key)
(4)遍历HashIterator
3、参考文档
1、HashMap数据结构
先结合源码来看。(备注:仅分析JDK8源码
Node<K,V>[] table;
int size;
int threshold;
float loadFactor;
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
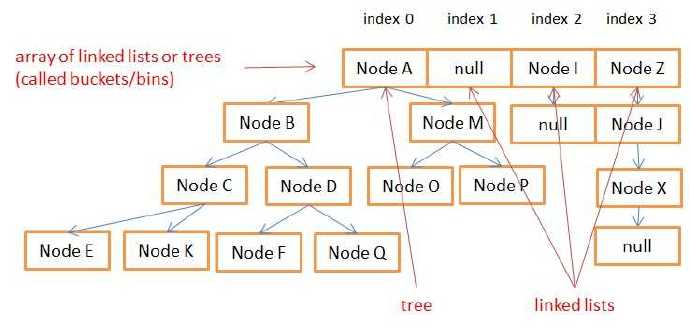
HashMap的结构图如上所示:
(1)内部包含一个数组,数组中每个元素可以认为是一个桶Bin,每个桶里对应一个单链表或红黑树。
(2)当某个桶里单链表结点数>=7,需要转换成红黑树结构
(3)当某个桶里红黑树结点数<=6,需要退化成单链表结构
从时间复杂度来分析,这样设计的优势:
假设单链表的长度为n,则查找某个结点的时间复杂度是O(n),而红黑树的时间复杂度是O(logn)
2、数据的增删改查
知道了整个结构图,我接下来有几个问题会比较好奇:
(1)怎么存数据?
(2)怎么取数据?
(3)怎么删数据?
(4)数据怎么遍历?
具体每一行代码注释,下面参考文档 [Java 容器源码分析之 HashMap] 的大佬讲的很好,直接看那个就行了。我自己只总结流程。
(1)存数据put(K key, V value)
基本逻辑:
1.计算key的hash值
2.根据i = (n - 1) & hash计算索引,得到在数组(桶)第几个位置
3.针对table[i],进行put操作,考虑如下情况:
- (1)若table[i]头结点p为空,则新建一个结点Node,作为table[i]头结点
- (2)若table[i]头结点满足
p.hash == hash && (p.key == key || key.equals(p.key)),则更新头结点的value - (3)若table[i]是红黑树,则走红黑树的put逻辑
- (4)若table[i]是单链表,则遍历单链表。若找到符合条件
p.hash == hash && (p.key == key || key.equals(p.key))的结点,则更新结点值;若没找到则新建一个结点添加到单链表结尾。
4.数据put后,相关扫尾操作:
- (1)若单链表长度>=7,调用
treeifyBin将单链表转化成红黑树 - (2)如果是更新结点,则针对被更新的结点,调用
afterNodeAccess(e)进行访问后处理 - (3)如果是添加结点,则size+1,且若size > threshold,调用
resize()进行扩容处理,之后调用afterNodeInsertion(evict)进行插入后处理
计算hash(key)的逻辑:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
扩容逻辑:
1.创建一个新数组newTab,其容量是旧数组oldTab的2倍,即newCap = oldCap « 1
2.依次遍历旧数组oldTab的每个元素e = oldTab[j],将其插入新数组newTab:
- (1)若e只有一个头结点,则计算插入newTab的位置
index = e.hash & (newCap - 1),并赋值给newTab[index] - (2)若e是红黑树,则将其拆分为hiHead,loHead 2个结构分别放到newTab[j]和newTab[j+oldCap]的2个位置
- (3)若e是含多个结点的单链表,则根据单链表的每个结点是否满足
(e.hash & oldCap) == 0划分为loHead和hiHead两个链表,并依次赋给newTab[j]和newTab[j + oldCap],即newTab[j] = loHead; newTab[j + oldCap] = hiHead;
几点需要注意的地方:
(1)数据存到哪个数组就用哪个数组的容量求索引,新数组用newCap,旧数组用oldCap
(2)扩容之后,新数组长度变大了,旧数组每个桶中的元素对半划分为2个结构,放到新数组的2个桶中。
(3)划分规则:原来求index是根据hash & (oldCap - 1),oldCap翻倍后相当于(oldCap - 1)左移1位,假设oldCap=1000,则扩容后为10000,index的范围是[0000-0111, 1000-1111],所以根据oldCap的最高位是1还是0来划分为2部分即可。
(2)取数据get(Object key)
基本逻辑:
1.计算key的hash值
2.根据i = (n - 1) & hash计算索引,得到在数组(桶)第几个位置
3.针对table[i],考虑如下情况:
- (1)若table[i]头结点p为空,则返null
- (2)若table[i]头结点p满足
p.hash == hash && (p.key == key || key.equals(p.key)),则返头结点p - (3)若table[i]是红黑树,则走红黑树的get逻辑
- (4)若table[i]是单链表,则遍历单链表找到满足
p.hash == hash && (p.key == key || key.equals(p.key))的结点并返回
(3)删数据remove(Object key)
删除单个结点逻辑:
和get逻辑差不多,无非是先找到结点,再去删除结点,删除之后size-1,如果结点在红黑树上,则根据size决定是否将红黑树退化成单链表,最后调一下afterNodeRemoval(node);做后续处理。
删除所有结点逻辑:
直接将数组每个元素置为null,size=0
public void clear() {
Node<K,V>[] tab;
modCount++;
if ((tab = table) != null && size > 0) {
size = 0;
for (int i = 0; i < tab.length; ++i)
tab[i] = null;
}
}
(4)遍历HashIterator
平常开发中遍历的时候,一般是调用集合的iterator()得到Iterator,然后调用Iterator的next()方法访问下一个元素。
我们看HashIterator源码:
abstract class HashIterator {
Node<K,V> next; // next entry to return
Node<K,V> current; // current entry
int expectedModCount; // for fast-fail
int index; // current slot
HashIterator() {
expectedModCount = modCount;
Node<K,V>[] t = table;
current = next = null;
index = 0;
if (t != null && size > 0) { // advance to first entry
do {} while (index < t.length && (next = t[index++]) == null);
}
}
public final boolean hasNext() {
return next != null;
}
final Node<K,V> nextNode() {
Node<K,V>[] t;
Node<K,V> e = next;
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
if (e == null)
throw new NoSuchElementException();
if ((next = (current = e).next) == null && (t = table) != null) {
do {} while (index < t.length && (next = t[index++]) == null);
}
return e;
}
}
在调用nextNode()的方法时,直接返回next。另外我们还需要提前把下一次访问的结点找到作为新的next。
基本逻辑:
1.根据当前的next,确定要返回的next结点
2.确定下一次访问时的current和next。current = next,next = ?,考虑如下情况:
- (1)如果next不是当前数组某个元素中的单链表或红黑树中最后一个结点,则next = next.next
- (2)如果next是当前数组某个元素中最后一个结点或者空结点,则转向数组下一个元素(下一个桶Bin),然后再在下一个Bin中遍历单链表或红黑树的结点作为新的next
这么看来遍历的规则就是:整体顺序是按照桶的index大小,同一个index的桶中按照单链表或红黑树的next指向去找next。
(5)扩容
扩容发生在put过程,当结点数量size > threshold时,会触发扩容。
threshold的确定规则:大小是2的k次幂。
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}